"1 ? 1 + 1 ? 1 +...", a curiosa explicação de matemático sobre como Deus criou o mundo

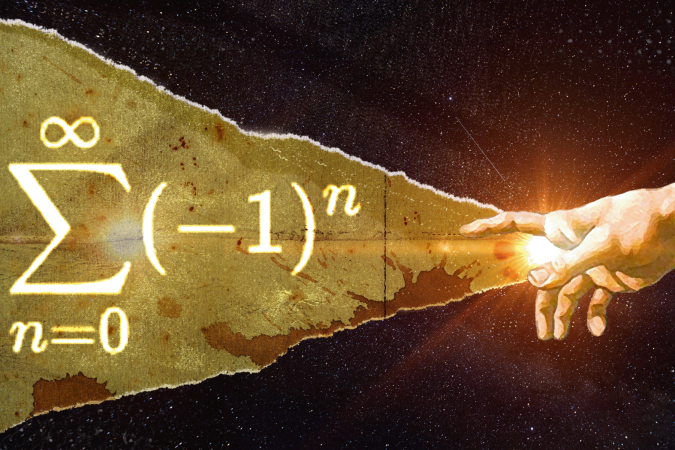
A matemática poderia explicar o significado da vida, do universo e de todo o resto?

Vai saber. Mas sempre vale tentar.

Uma das tentativas de demonstrar a probabilidade de algo tão desconcertante como o início de tudo foi com algo que está representado como você vê na imagem acima.

Com ∑, ∞ e vários n pode parecer um pouco intimidador.

Mas tudo isso pode ser representado de outra forma: 1 − 1 + 1 − 1 +…

São operações simples, mas se as repetirmos ao infinito, tornam-se uma soma que ocupou os maiores matemáticos desde o século 18.

A grande questão era: qual é o resultado dessa soma infinita?

Uma resposta intuitivamente óbvia é que não há resposta: se continuar infinitamente, se alterará entre 0 e 1 sem nunca chegar a valor único.

No entanto, essa é apenas uma das 4 opções consideradas ao longo do tempo.

E talvez a mais surpreendente seja que a que mais convenceu o primeiro matemático a chamar a atenção para este quebra-cabeça conhecido como série Grandi.

Luigi Guido Grandi (1671 - 1742) foi um padre, filósofo, matemático e engenheiro nascido em Cremona, hoje na Itália.

Seu interesse pela matemática demorou a surgir, mas com seu primeiro livro, "Geometrica divinatio Vivianeorum problematum", publicado em 1699, ele ganhou reconhecimento no seu e em outros países.

Sua reputação o levaria a virar, em 1707, o matemático da corte do Grão-Duque da Toscana, Cosme 3º de Medici, e no cargo foi responsável por importantes projetos de engenharia, incluindo a drenagem do Vale de Chianna.

Também colaborou na publicação da primeira edição das obras de Galileu Galilei (1718), publicou uma versão italiana dos "Elementos" de Euclides (1731), aconselhou o Papa Clemente sobre a reforma do calendário e introduziu na Itália as ideias de Gottfried Leibniz sobre cálculo.

Admirado também no exterior, tornou-se membro da prestigiada Royal Society of London em 1709, depois de Isaac Newton publicar seu trabalho sobre teoria musical.

Uma de suas obras mais admiradas foi o estudo da rosa polar, uma família de curvas que lembram flores, que chamou de rhodoneas (do grego rhodon, rosa), em seu livro "Flores Geometrici" (1725).

Mas foi uma outra obra sua que despertou não só o interesse de seus pares, mas também uma acalorada polêmica em torno da série que leva seu nome.

O livro, publicado em 1703 e com o título de “Quadratura do Círculo e da Hipérbole”, continha um resultado que chamou bastante atenção.

Grandi estudou aquela soma infinita de 1 − 1 + 1 − 1 + · · ·

E observou que adicionando parênteses, chegava-se a resultados diferentes.

(1 - 1) + (1 - 1) + (1 - 1)... resultava em 0 + 0 + 0..., que é igual a 0.

Mas se fosse escrito assim: 1 + (- 1 + 1) + (- 1 + 1) + (- 1 + 1)... então a soma seria 1 + 0 + 0 + 0..., o que daria 1.

Isso por si só já era surpreendente.

Mais surpreendente ainda foi ele afirmar que a soma de infinitos 0s é igual a 1/2.

Grandi preferiu explicar esse resultado com uma parábola em que imaginava dois irmãos que herdaram dos pais uma joia valiosa.

Eles foram proibidos de vendê-la e dividi-la à metade destruiria seu valor.

Os irmãos concordaram que alternariam a propriedade da joia, trocando todo dia de Ano Novo.

Supondo que o acordo continuasse indefinidamente, então, do ponto de vista de cada irmão, a propriedade da joia pode ser representada pela série

1 − 1 + 1 − 1 + · · ·

Assim, cada irmão possui a joia pela metade do tempo, então o valor desta série seria 1/2.

Você pode ficar surpreso, mas vários matemáticos relevantes da época concordaram que essa era a resposta.

O renomado Leibniz chegou à mesma conclusão por outros métodos e declarou que 1/2 era a resposta que lhe parecia correta, embora reconhecesse que o argumento era mais "metafísico do que matemático".

O suíço Leonhard Euler, um dos maiores e mais prolíficos matemáticos de todos os tempos, fez seus próprios cálculos e escreveu em 1760:

“Não pode restar dúvida de que, de fato, a série 1 − 1 + 1 − 1 + 1 − 1 + etc. e a fração 1/2 são quantidades equivalentes e que é sempre permitido substituir uma pela outra sem erro."

Tal como eles, outros matemáticos em toda a Europa discutiram a série infinita, chegando a suas próprias conclusões.

Mas um deles, em particular, não gostou muito das ideias de Grandi.

Alessandro Marchetti (1633 - 1714) era o professor de matemática na Universidade de Pisa e ressentiu-se da fama internacional de Grandi.

Tentando desacreditá-lo, criticou duramente seu livro.

Em resposta, Grandi publicou uma segunda edição de "Quadratura..." em 1710.

Mas desta vez ele foi autorizado a incluir um comentário que os censores haviam exigido que fosse removido da versão anterior, condição com a qual ele concordou, não sem relutância.

Era uma afirmação ainda mais surpreendente do que os resultados que ele tinha obtido.

Sua reflexão foi de que ao se adicionar parênteses à expressão 1 − 1 + 1 − 1 + · · · era possível obter, de maneiras diferentes, 1 ou 0, “então a ideia de criação ex nihilo era perfeitamente plausível”.

A criação ex nihilo é a criação a partir do nada.

Além disso, se uma quantidade finita podia ser obtida a partir de uma soma infinitamente prolongada de zeros, era necessário “reconhecer aquele poder infinito”, uma força que mesmo “multiplicando o que em si não é nada, transforma-o em algo, da mesma forma que, dividindo uma magnitude finita, força-a a degenerar em nada."

E tinha sido “pelo poder infinito do Deus Criador que todas as coisas foram feitas do nada, e todas as coisas podem ser reduzidas ao nada”.

Assim, Grandi parecia ter chegado a uma prova matemática de que Deus havia criado tudo do nada.

É claro que isso serviu para jogar lenha na fogueira: Marchetti publicou então um ataque a essa segunda edição em 1711, ao qual Grandi respondeu com outro artigo em 1712.

A polêmica continuou até a morte de Marchetti, em 1714.

O interesse pela série de Grandi, no entanto, persistiu.

Embora seus argumentos não resistam ao escrutínio matemático moderno, existe um marco para somas infinitas em que a série de Grandi é igual a 1/2.

É conhecida como soma de Cesàro, em homenagem ao matemático italiano Ernesto Cesàro, do final do século XIX.

No entanto,segundo diversas fontes, a opinião geral dos matemáticos hoje é que o valor da série de Grandi não é 1, nem 0, nem 1/2: o resultado dessa soma infinita é nenhum.

Mas, se fosse algum, seria 1/2.

Fonte: correiobraziliense

Participe do nosso grupo no whatsapp clicando nesse link

Participe do nosso canal no telegram clicando nesse link

Assine nossa newsletter

Email CONFIRMAR